棋盘覆盖问题

棋盘覆盖问题

题目描述

给定一个大小为$2^k∗2^k$（也就是2∗2或4∗4或8∗8或16∗16等，依次类推）的白色棋盘，其中有一个格子是黑色的。下图为k=2即4∗4的棋盘示例。

现在想用一种大小占三个小方格的L形骨牌来覆盖整个棋盘，这种L形骨牌可以通过旋转得到下面四种形态：

注意，在覆盖的时候，骨牌之间不能相互覆盖，也不能覆盖初始状态下已经是黑色的那个格子。

请输出覆盖方案，下图是上面示例的覆盖方案（注：不同颜色只是用来区分不同的骨牌，与题意无关）。

输入描述

第一行为三个正整数k、cx、cy（1≤k≤8、1≤cx≤$2^k$、1≤cy≤$2^k$），分别表示棋盘的边长是2k、初始黑色的格子坐标是(cx,cy)。其中以最左下的方格坐标为(1,1)，向右为x增加方向，向上为y增加方向。

输出描述

每行输出一块骨牌的信息，即该骨牌的拐角方格的坐标(x,y)，题目描述中的四种形态的拐角方格分别是左上、右上、左下、右下的方格。输出骨牌的顺序为，优先输出x较小的骨牌，x相同的优先输出y较小的骨牌。

样例1

输入：

1 2 1

输出：

1 2

样例2

输入：

2 2 3

输出：

题解

Reference:
棋盘覆盖问题
浅谈棋盘覆盖问题(算法思想及伪代码)
算法分析与设计：棋盘覆盖问题（分治法）

主要思想：

把棋盘从中心划分为四个小棋盘
首先用骨牌覆盖中心位置，这个位置坐标由黑色方块所在的小棋盘位置所决定
由于第2步在中心覆盖了骨牌，所以现在每个小棋盘都有黑色方块（覆盖的骨牌即为黑色方块）
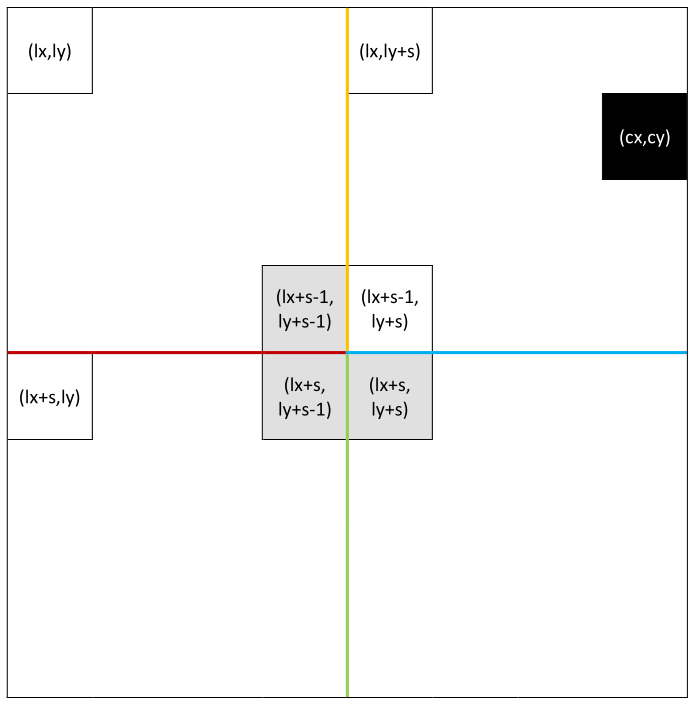
- 新增小棋盘黑色方块如下图灰色区域所示，坐标为：(lx+s-1, ly+s-1), (lx+s, ly+s-1), (lx+s, ly+s)
然后重复1、2、3步，直到棋盘大小为1。

棋盘分割和各个关键位置坐标图：

#include<iostream>
#include<vector>
#include<algorithm>
#include<utility>
#include<cmath>

using namespace std;

vector<pair<int, int> > res; // 每个覆盖在棋盘的骨牌拐角方格坐标(x, y); 

// sz: 棋盘大小(size); (lx, ly): 棋盘左上角位置坐标(left x, left y); (cx, cy): 固定黑色方格位置(const x, const y)
void chessBoard(int sz, int lx, int ly, int cx, int cy) {
    if (sz == 1) return; // 边界条件
    int s = sz / 2; // 分割棋盘的大小
    
    // 这里已经将棋盘分割为了4个小棋盘，分别为左上、右上、左下、右下棋盘；
    // 依次检查固定黑色方格位置
    // 是否在左上棋盘？
    if (cx < lx + s && cy < ly + s) {
        res.emplace_back(lx + s, ly + s); // 棋盘分割中心，骨牌覆盖的坐标
        chessBoard(s, lx, ly, cx, cy);
    } else {
        chessBoard(s, lx, ly, lx + s - 1, ly + s - 1); // 如果不是, 设置右下角为固定黑色方格, 继续分割
    }

    // 是否在右上棋盘？
    if (cx < lx + s && cy >= ly + s) {
        res.emplace_back(lx + s, ly + s - 1);
        chessBoard(s, lx, ly + s, cx, cy);
    } else {
        chessBoard(s, lx, ly + s, lx + s - 1, ly + s);
    }

    // 是否在左下棋盘？
    if (cx >= lx + s && cy < ly + s) {
        res.emplace_back(lx + s - 1, ly + s);
        chessBoard(s, lx + s, ly, cx, cy);
    } else {
        chessBoard(s, lx + s, ly, lx + s, ly + s - 1);
    }

    // 是否在右下棋盘？
    if (cx >= lx + s && cy >= ly + s) {
        res.emplace_back(lx + s - 1, ly + s - 1);
        chessBoard(s, lx + s, ly + s, cx, cy);
    } else {
        chessBoard(s, lx + s, ly + s, lx + s, ly + s);
    }
}

int main() {
    int k, cx, cy;
    scanf("%d%d%d", &k, &cx, &cy);
    chessBoard(int(pow(2, k)), 1, 1, cx, cy);
    sort(res.begin(), res.end());
    for (auto &p : res) {
        printf("%d %d\n", p.first, p.second);
    }
    return 0;
}