A1162 Postfix Expression (25 分)

A1162 Postfix Expression (25 分)

Given a syntax tree (binary), you are supposed to output the corresponding postfix expression, with parentheses reflecting the precedences of the operators.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤ 20) which is the total number of nodes in the syntax tree. Then N lines follow, each gives the information of a node (the i-th line corresponds to the i-th node) in the format:

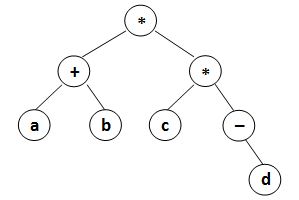
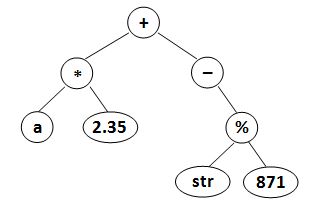
data left_child right_child

where data is a string of no more than 10 characters, left_child and right_child are the indices of this node's left and right children, respectively. The nodes are indexed from 1 to N. The NULL link is represented by −1. The figures 1 and 2 correspond to the samples 1 and 2, respectively.

Figure 1	Figure 2

Output Specification:

For each case, print in a line the postfix expression, with parentheses reflecting the precedences of the operators.There must be no space between any symbols.

Sample Input 1:

8
* 8 7
a -1 -1
* 4 1
+ 2 5
b -1 -1
d -1 -1
- -1 6
c -1 -1

Sample Output 1:

(((a)(b)+)((c)(-(d))*)*)

Sample Input 2:

8
2.35 -1 -1
* 6 1
- -1 4
% 7 8
+ 2 3
a -1 -1
str -1 -1
871 -1 -1

Sample Output 2:

(((a)(2.35)*)(-((str)(871)%))+)

题目大意：

给定一个二叉树，输出相应的后缀表达式，圆括号反映操作符的优先级。

思路

1. 根据输入数据找到根结点root（没有在左右孩子出现的结点就是根结点）
2. 写一个递归后序遍历，遍历过程中输出结果

注意：没有左子树但有右子树的子树，应要先输出字数的根结点，再输出右子树

AC代码

#include <bits/stdc++.h>
using namespace std;

struct node{
    string data;
    int lchild, rchild;
}tree[25];
bool notRoot[25] = {false};

void postTravel(int root) {
    if (root == -1) return;
    cout << "(" ;
    if (tree[root].lchild == -1 && tree[root].rchild != -1) {
        cout << tree[root].data;
        postTravel(tree[root].rchild);
        cout << ")";
        return;
    } else {
        postTravel(tree[root].lchild);
        postTravel(tree[root].rchild);
    }
    cout << tree[root].data << ")";
}

int main() {
    int n;
    scanf("%d\n", &n);
    string data;
    int l, r;
    for (int i = 1; i <= n; ++i) {
        cin >> data >> l >> r;
        tree[i] = node{data, l, r};
        notRoot[l] = true;
        notRoot[r] = true;
    }
    int root;
    for (int i = 1; i <= n; ++i) {
        if (!notRoot[i]) {
            root = i;
            break;
        }
    }
    postTravel(root);
    return 0;
}