202006-1 线性分类器

【题目描述】

\ 考虑一个简单的二分类问题——将二维平面上的点分为$A $和$B$ 两类。
\ 训练数据包含$n $个点，其中第$i $个点$(1 \le i \leq n)$可以表示为一个三元组$(x_i, y_i, type_i)$，即该点的横坐标、纵坐标和类别。
在二维平面上，任意一条直线可以表示为$θ_0 + θ_1x + θ_2y = 0 $的形式，即由$θ_0、θ_1 和
θ_2 $三个参数确定该直线，且满足$θ_1、θ_2$ 不同时为$0$。
基于这$n $个已知类别的点，我们想要在平面上找到一条直线作为一个线性分类器。具体来说，这条线要把训练数据中的$A、B $两类点完. 美. 分. 隔. 开来，即一侧只有$A $类点、另一侧只有$B $类点。这样，对于任意一个的未知类别的点，我们就可以根据它是位于直线的哪一侧来预测它的类别了。
在本题中我们仅需要处理$m $个如下查询：给定一条直线，判断它是否能将训练数据中的$A、B$ 两类点完美分开。

【输入格式】

从标准输入读入数据。
输入共$n + m + 1 $行。
第一行包含用空格分隔的两个正整数$n 和m$，分别表示点和查询的个数。
第二行到第$n + 1 $行依次输入$n $个点的信息。第$i + 1 $行$(1 \leq i \leq n)$包含用空格分隔的三项$x_i、y_i 和type_i$，分别表示第$i $个点的横、纵坐标和类别，其中坐标为整数、类别为一个大写英文字母$A 或B$。
第$n + 2$ 行到第$n + m + 1 $行依次输入$m $个查询。第$j + n + 1 $行$(1 \leq j \leq m)$包含用空格分隔的三个整数$θ_0、θ_1 和θ_2$，表示第$j$ 个查询中给定直线的三个参数。

【输出格式】

输出到标准输出。
输出共$m $行，每行输出一个字符串。
第$j $行$(1 ≤ j ≤ m)$输出的字符串对应第$j$个查询的结果：如果给定直线可以完
美分隔$A、B$ 两类点，则输出$Yes$；否则输出$No$。

【样例1 输入】

【样例1 输出】

No
No
Yes

【样例1 解释】

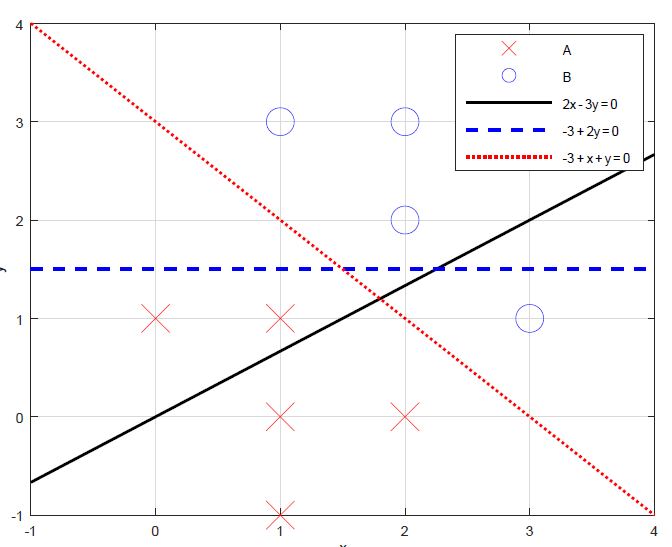
只有第3 个查询给出的直线能将$A、B $两类点完美分隔。

【子任务】

输入数据保证不存在恰好落在给定直线上的点；
$0 < n ≤ 10^3、0 < m ≤ 20，$且$A、B $两类点的数量均不为$0$；
所有点的坐标和给定直线的三个参数均为整数，且绝对值$≤ 10^6$；
任意两个点的坐标不完全相同。

【解题程序】

#输入
n, m = map(int, input().split())
class_A = []
class_B = []
for _ in range(n):
    t = input().split()
    if t[-1] == 'A':
        class_A.append(list(map(int, t[:2])))
    else:
        class_B.append(list(map(int, t[:2])))

#判断这一类的点是否被直线完美分割
def judge_class(a, b, c, class_):
    for point in class_:
        lineValue = a + b * point[0] + c * point[1]
        pointValue = lineValue > 0
        try:
            if pointValue != preValue:
                #若现在的值与前一个值不等，则不是完美分割
                return False
        except NameError:
            #第一个点没有前一个值，会报错
            pass
        preValue = pointValue #记录前一个值
    #完美分割一个类
    return True

for _ in range(m):
    #给定直线的三个参数
    a, b, c = map(int, input().split())
    flag = 1
    for class_ in (class_A, class_B):
        judge = judge_class(a, b, c, class_)
        if not judge:
            flag = 0
            print("No")
            break
    if flag:
        print("Yes")

Eighty Percent